Density, distribution function, quantile function,
random generation and hazard function for the Marshall-Olkin Extended Inverse Weibull distribution
with parameters mu, sigma and nu.
Usage
dMOEIW(x, mu, sigma, nu, log = FALSE)
pMOEIW(q, mu, sigma, nu, lower.tail = TRUE, log.p = FALSE)
qMOEIW(p, mu, sigma, nu, lower.tail = TRUE, log.p = FALSE)
rMOEIW(n, mu, sigma, nu)
hMOEIW(x, mu, sigma, nu)Arguments
- x, q
vector of quantiles.
- mu
parameter.
- sigma
parameter.
- nu
parameter.
- log, log.p
logical; if TRUE, probabilities p are given as log(p).
- lower.tail
logical; if TRUE (default), probabilities are P[X <= x], otherwise, P[X > x].
- p
vector of probabilities.
- n
number of observations.
Value
dMOEIW gives the density, pMOEIW gives the distribution
function, qMOEIW gives the quantile function, rMOEIW
generates random deviates and hMOEIW gives the hazard function.
Details
The Marshall-Olkin Extended Inverse Weibull distribution mu,
sigma and nu has density given by
\(f(x) = \frac{\mu \sigma \nu x^{-(\sigma + 1)} exp\{{-\mu x^{-\sigma}}\}}{\{\nu -(\nu-1) exp\{{-\mu x ^{-\sigma}}\} \}^{2}},\)
for x > 0.
References
Hassan M O, A.H E, A.M.K T, Abdulkareem M Bc (2017). “Extended inverse Weibull distribution with reliability application.” Journal of the Egyptian Mathematical Society, 25, 343--349. doi:10.1016/j.joems.2017.02.006 , http://dx.doi.org/10.1016/j.joems.2017.02.006.
Author
Amylkar Urrea Montoya, amylkar.urrea@udea.edu.co
Examples
old_par <- par(mfrow = c(1, 1)) # save previous graphical parameters
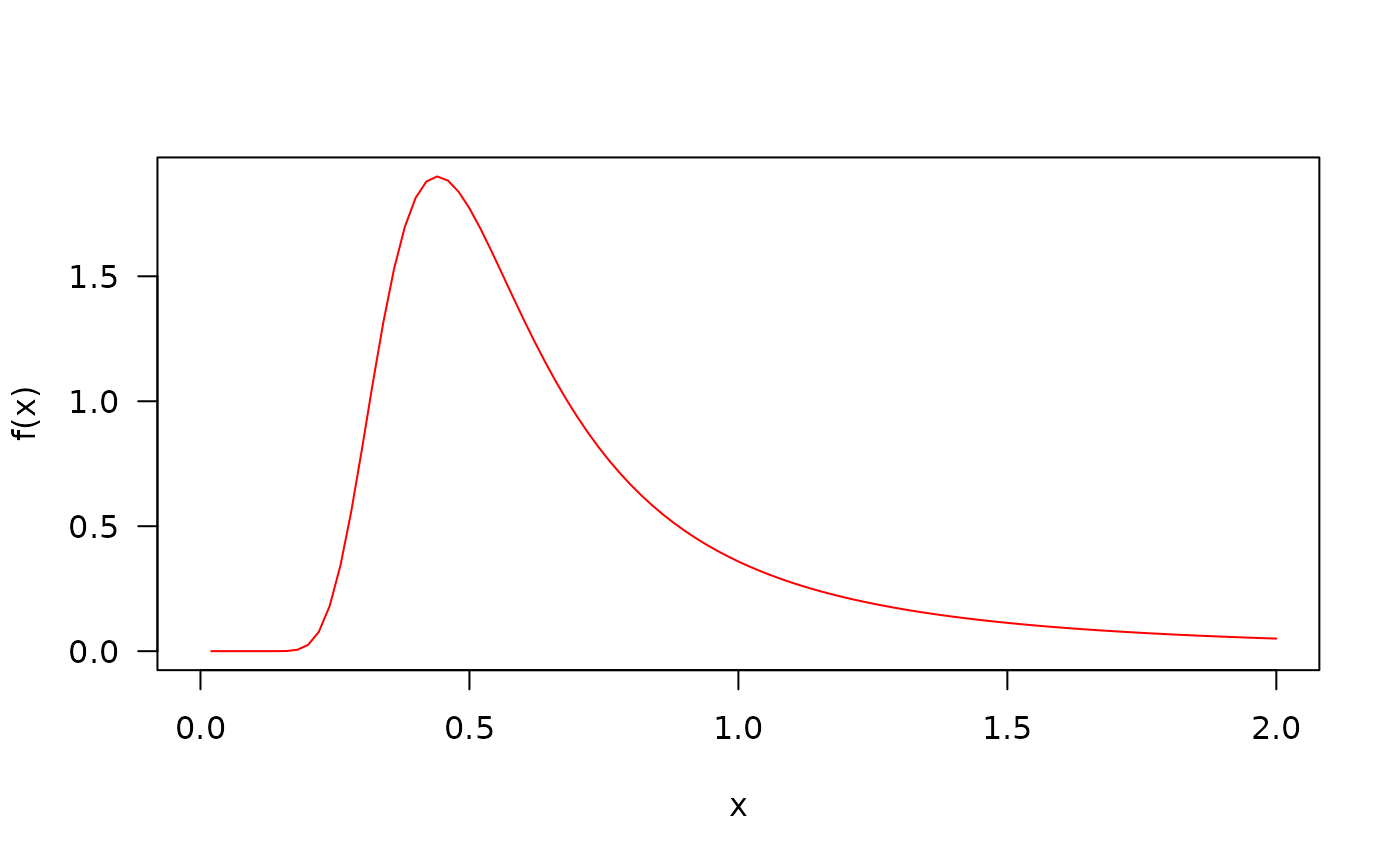
## The probability density function
curve(dMOEIW(x, mu=0.6, sigma=1.7, nu=0.3), from=0, to=2,
col="red", ylab="f(x)", las=1)
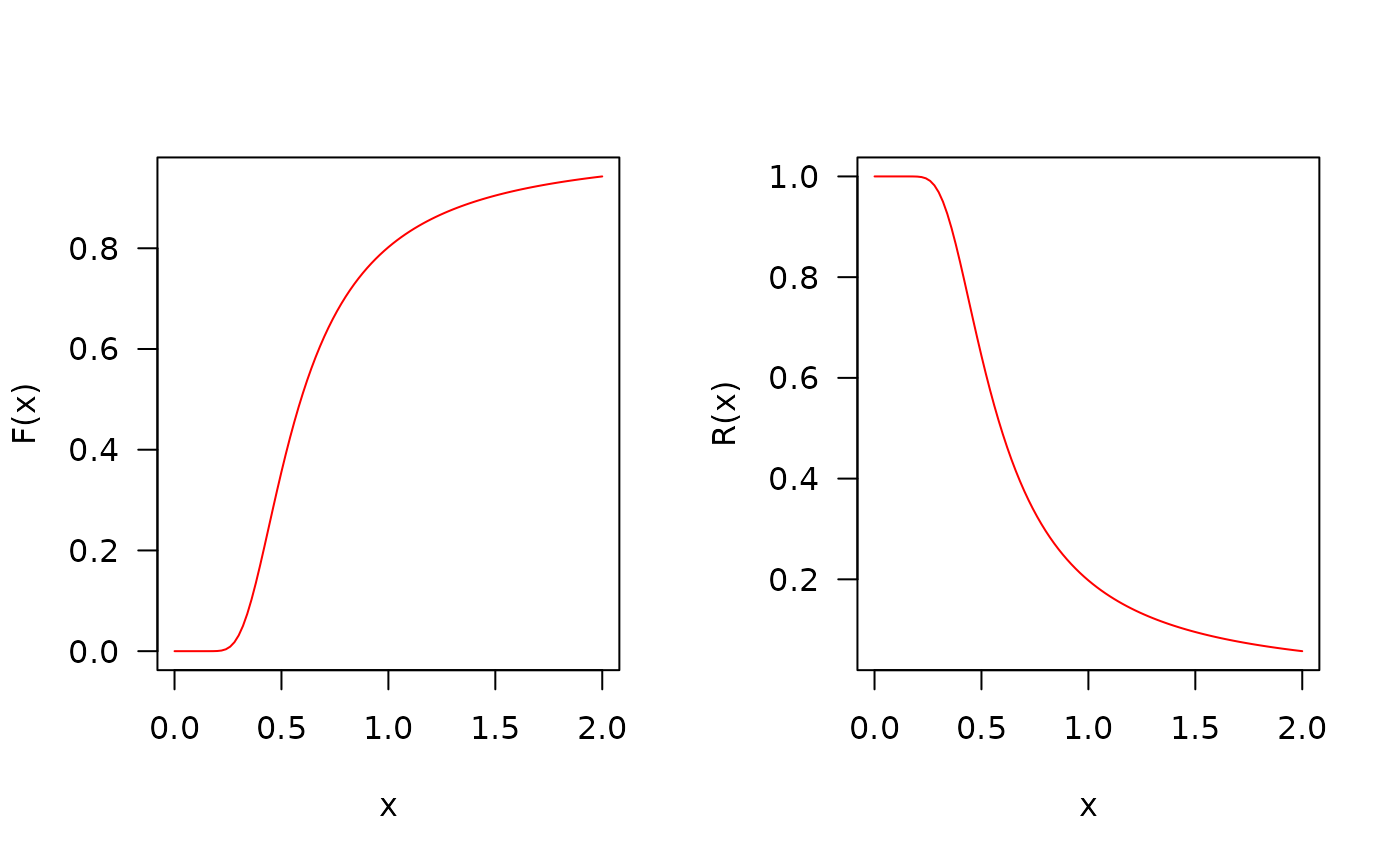
## The cumulative distribution and the Reliability function
par(mfrow=c(1, 2))
curve(pMOEIW(x, mu=0.6, sigma=1.7, nu=0.3),
from=0.0001, to=2, col="red", las=1, ylab="F(x)")
curve(pMOEIW(x, mu=0.6, sigma=1.7, nu=0.3, lower.tail=FALSE),
from=0.0001, to=2, col="red", las=1, ylab="R(x)")
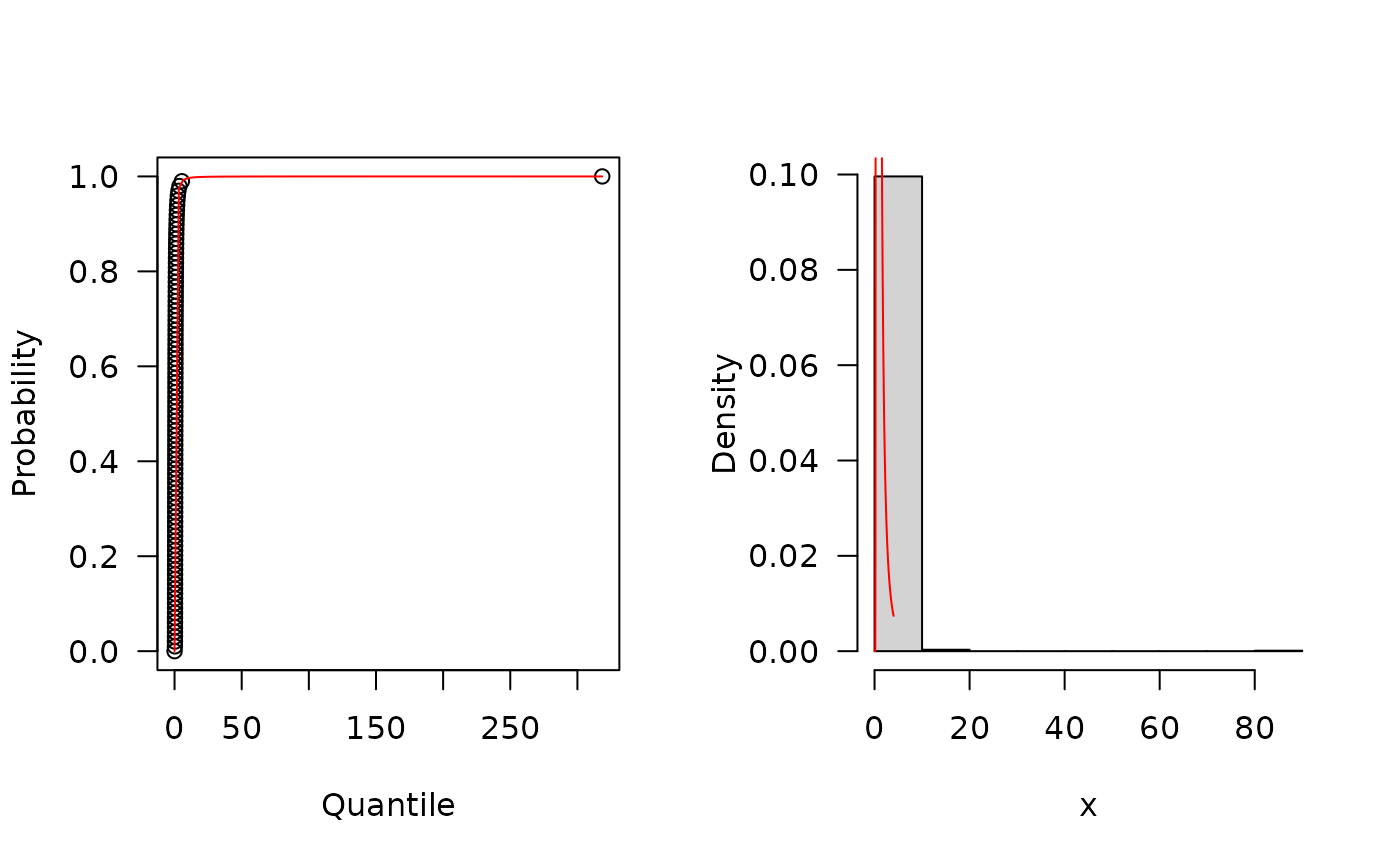
## The quantile function
p <- seq(from=0, to=0.99999, length.out=100)
plot(x=qMOEIW(p, mu=0.6, sigma=1.7, nu=0.3), y=p, xlab="Quantile",
las=1, ylab="Probability")
curve(pMOEIW(x, mu=0.6, sigma=1.7, nu=0.3),
from=0, add=TRUE, col="red")
## The random function
hist(rMOEIW(n=1000, mu=0.6, sigma=1.7, nu=0.3), freq=FALSE,
xlab="x", las=1, main="")
curve(dMOEIW(x, mu=0.6, sigma=1.7, nu=0.3),
from=0.001, to=4, add=TRUE, col="red")
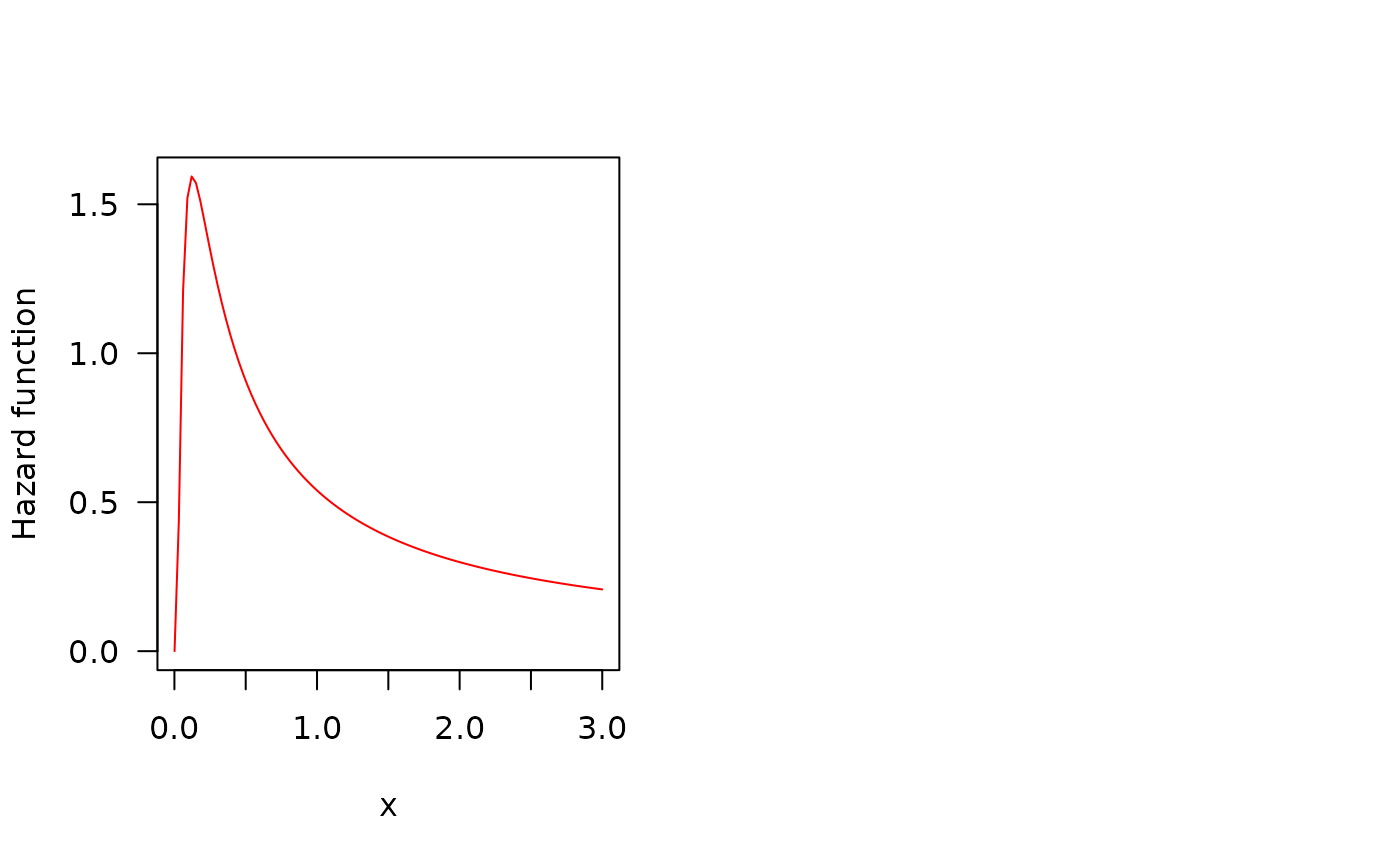
## The Hazard function
curve(hMOEIW(x, mu=0.5, sigma=0.7, nu=1), from=0.001, to=3,
col="red", ylab="Hazard function", las=1)
par(old_par) # restore previous graphical parameters
