OW distribution

library(RelDists)
#> Loading required package: survival
#> Loading required package: EstimationTools
#> Loading required package: DEoptim
#> Loading required package: parallel
#> 
#> DEoptim package
#> Differential Evolution algorithm in R
#> Authors: D. Ardia, K. Mullen, B. Peterson and J. Ulrich
#> Loading required package: BBmisc
#> 
#> Attaching package: 'BBmisc'
#> The following object is masked from 'package:base':
#> 
#>     isFALSE
#> Loading required package: GA
#> Loading required package: foreach
#> Loading required package: iterators
#> Package 'GA' version 3.2.4
#> Type 'citation("GA")' for citing this R package in publications.
#> 
#> Attaching package: 'GA'
#> The following object is masked from 'package:utils':
#> 
#>     de
#> Loading required package: gaussquad
#> Loading required package: orthopolynom
#> 
#> 
#> ><<<<<<<<<<<<<<<<<<<<<<<<   EstimationTools Version 4.0.0   >>>>>>>>>>>>>>>>>>>>>>>><
#>   Feel free to report bugs in https://github.com/Jaimemosg/EstimationTools/issues
library(EstimationTools)
library(gamlss)
#> Loading required package: splines
#> Loading required package: gamlss.data
#> 
#> Attaching package: 'gamlss.data'
#> The following object is masked from 'package:datasets':
#> 
#>     sleep
#> Loading required package: gamlss.dist
#> Loading required package: nlme
#> 
#> Attaching package: 'nlme'
#> The following object is masked from 'package:BBmisc':
#> 
#>     collapse
#>  **********   GAMLSS Version 5.4-22  **********
#> For more on GAMLSS look at https://www.gamlss.com/
#> Type gamlssNews() to see new features/changes/bug fixes.

Odd Weibull distribution

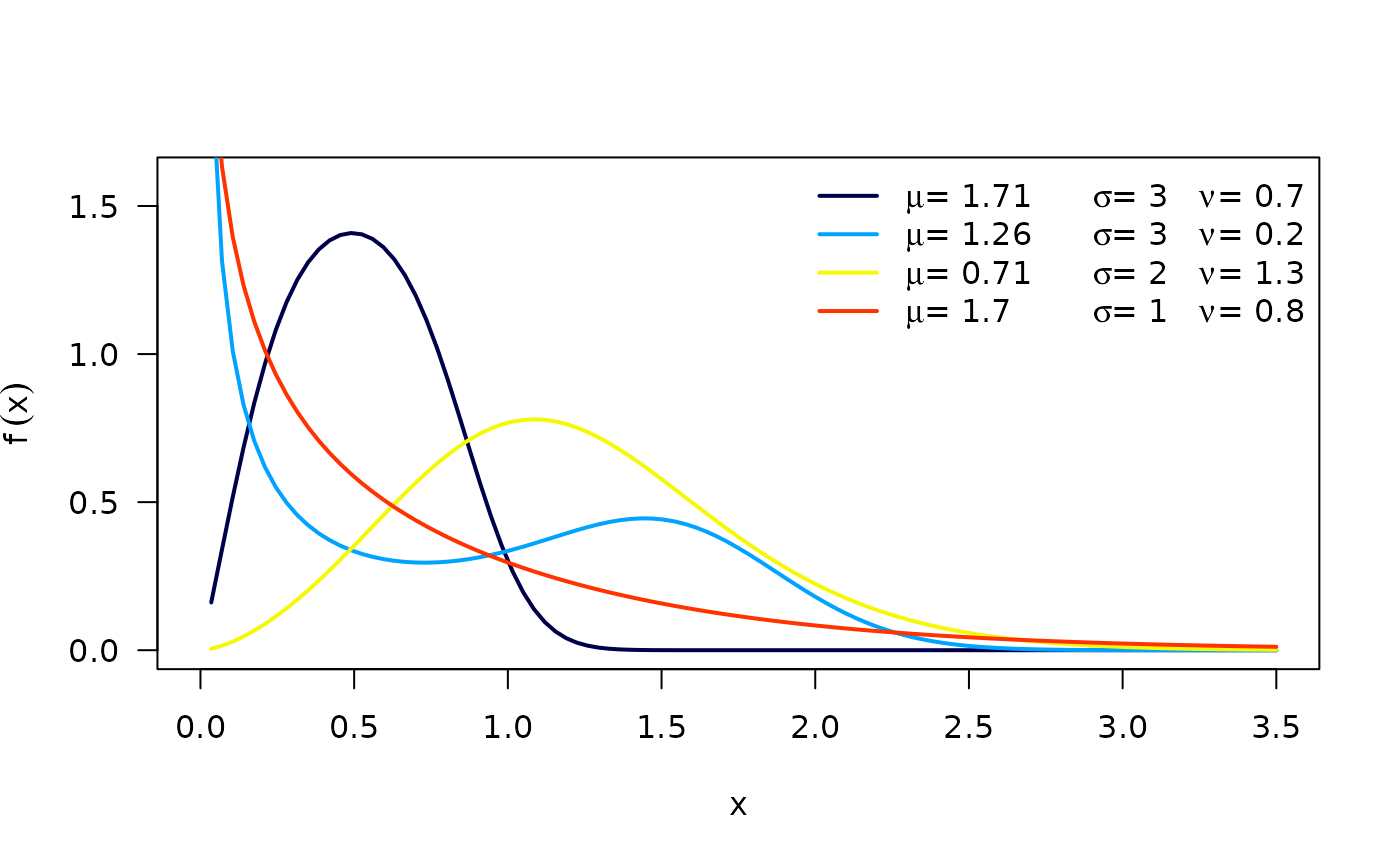
This distribution was proposed by Cooray (2006). The probability density function $f(x)$ and cumulative density function $F(x)$ are given by:

$f(x) = \left( \frac{\sigma\nu}{x} \right) (\mu x)^\sigma e^{(\mu x)^\sigma} \left(e^{(\mu x)^{\sigma}}-1\right)^{\nu-1} \left[ 1 + \left(e^{(\mu x)^{\sigma}}-1\right)^\nu \right]^{-2},$

and

$F(x) = 1 - \left[ 1 + \left( e^{(\mu x)^{\sigma}} - 1 \right)^\nu \right]^{-1}, \quad x>0,$

respectively, where $\mu>0, \quad \sigma\nu>0$ . $\mu$ is the scale parameter, $\sigma$ and $\nu$ are the shape parameters. Next figure shows possible shapes of the $f(x)$ and $F(x)$ for several values of the parameters.

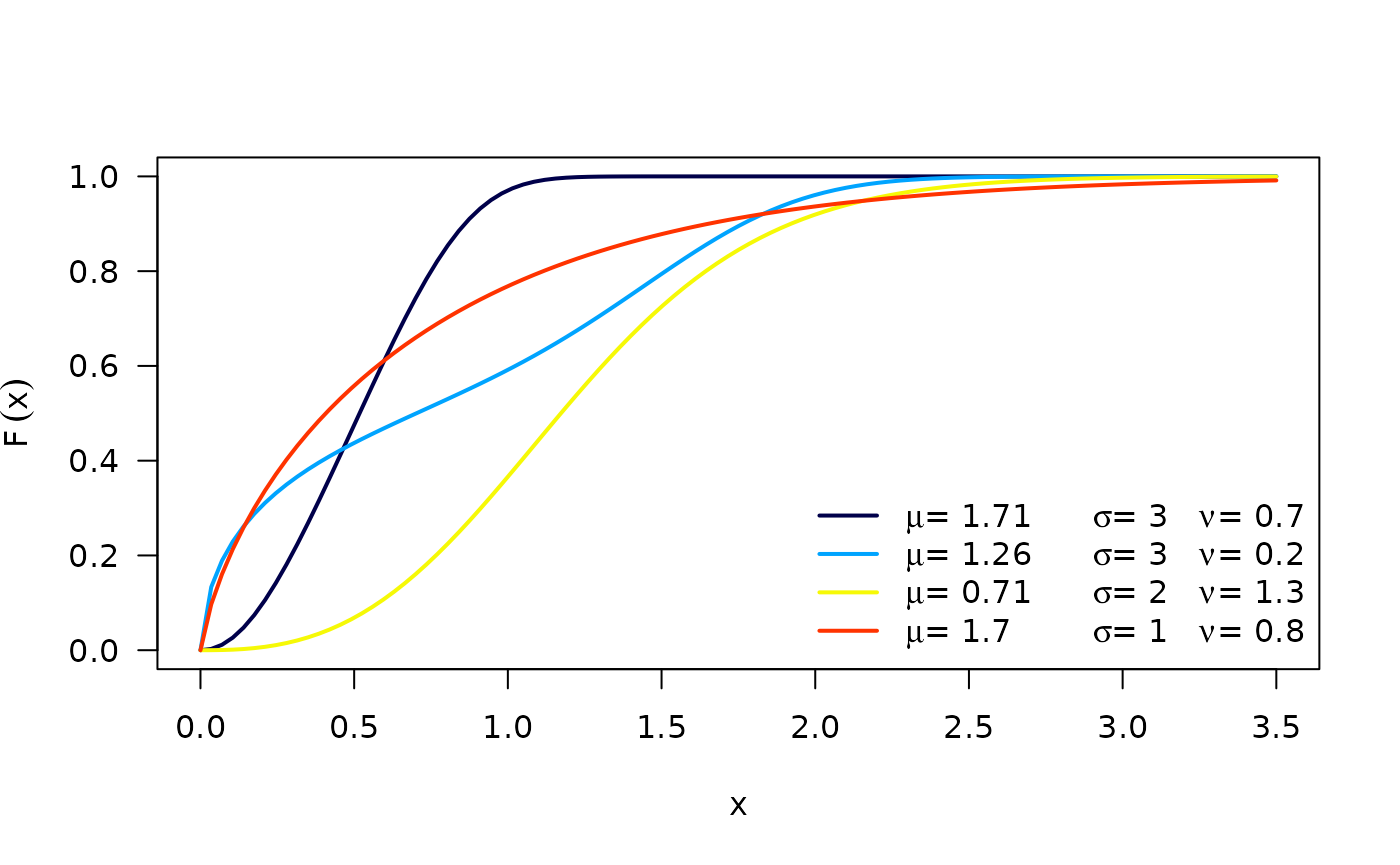
The hazard function (hf) of the OW distribution is:

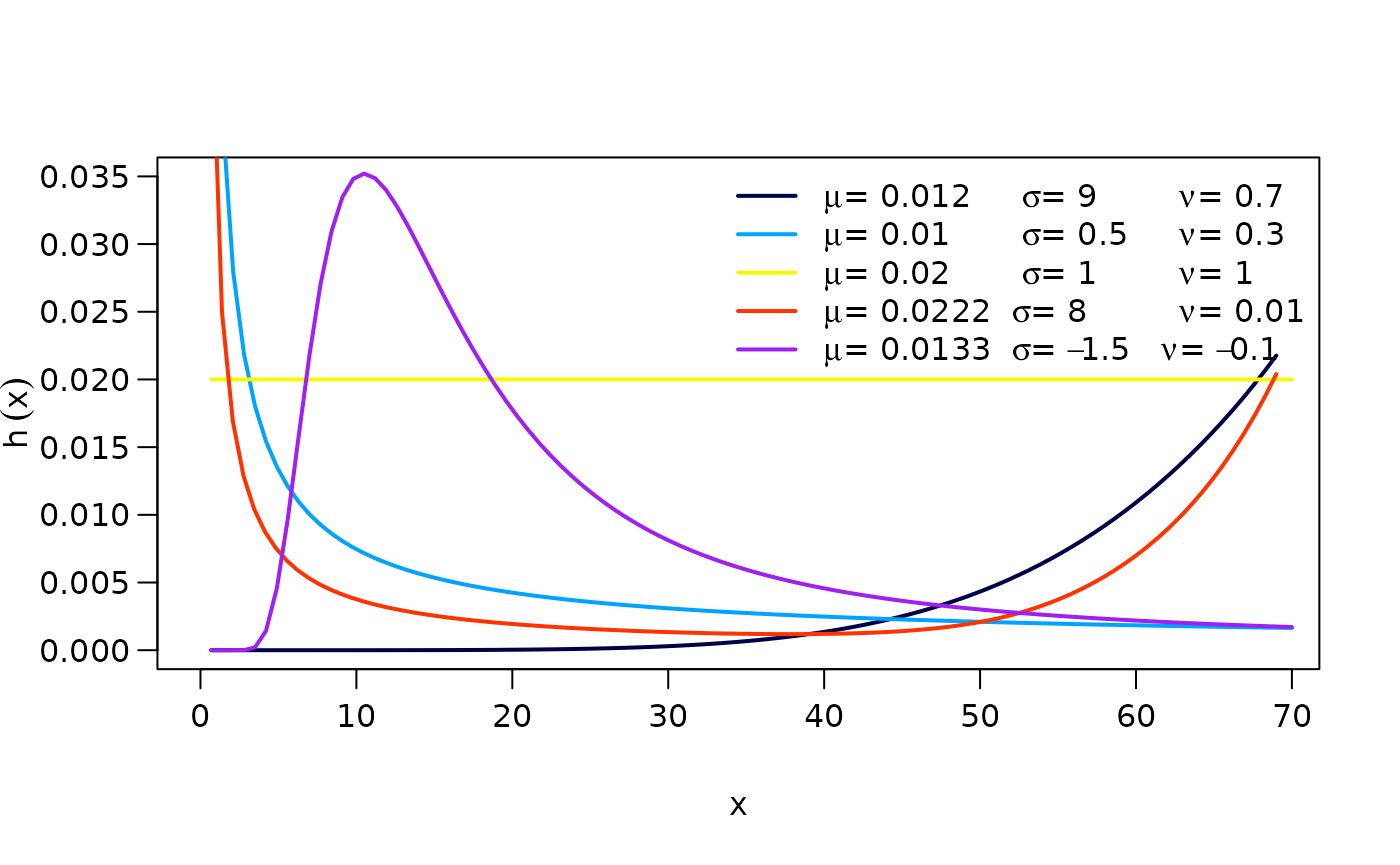
$h(x) = \left( \frac{\sigma\nu}{x} \right) (\mu x)^\sigma e^{(\mu x)^\sigma} \left(e^{(\mu x)^{\sigma}}-1\right)^{\nu-1} \left[ 1 + \left(e^{(\mu x)^{\sigma}}-1\right)^\nu \right]^{-1}, x>0,$

where the hf can take the following shapes:

Increasing if $\sigma>1$ and $\sigma\nu>1$ .
Decreasing if $\sigma<1$ and $\sigma\nu<1$ .
Unimodal shaped if either $\sigma<0$ and $\nu<0$ or $\sigma<1$ and $\sigma\nu\geq 1$ .
Bathtub shaped if $\sigma>1$ and $\sigma\nu\geq 1$ .

The figure shows possible shapes of the hf mentioned above:

The following figure illustrate the regions corresponding to the different hazard shapes:

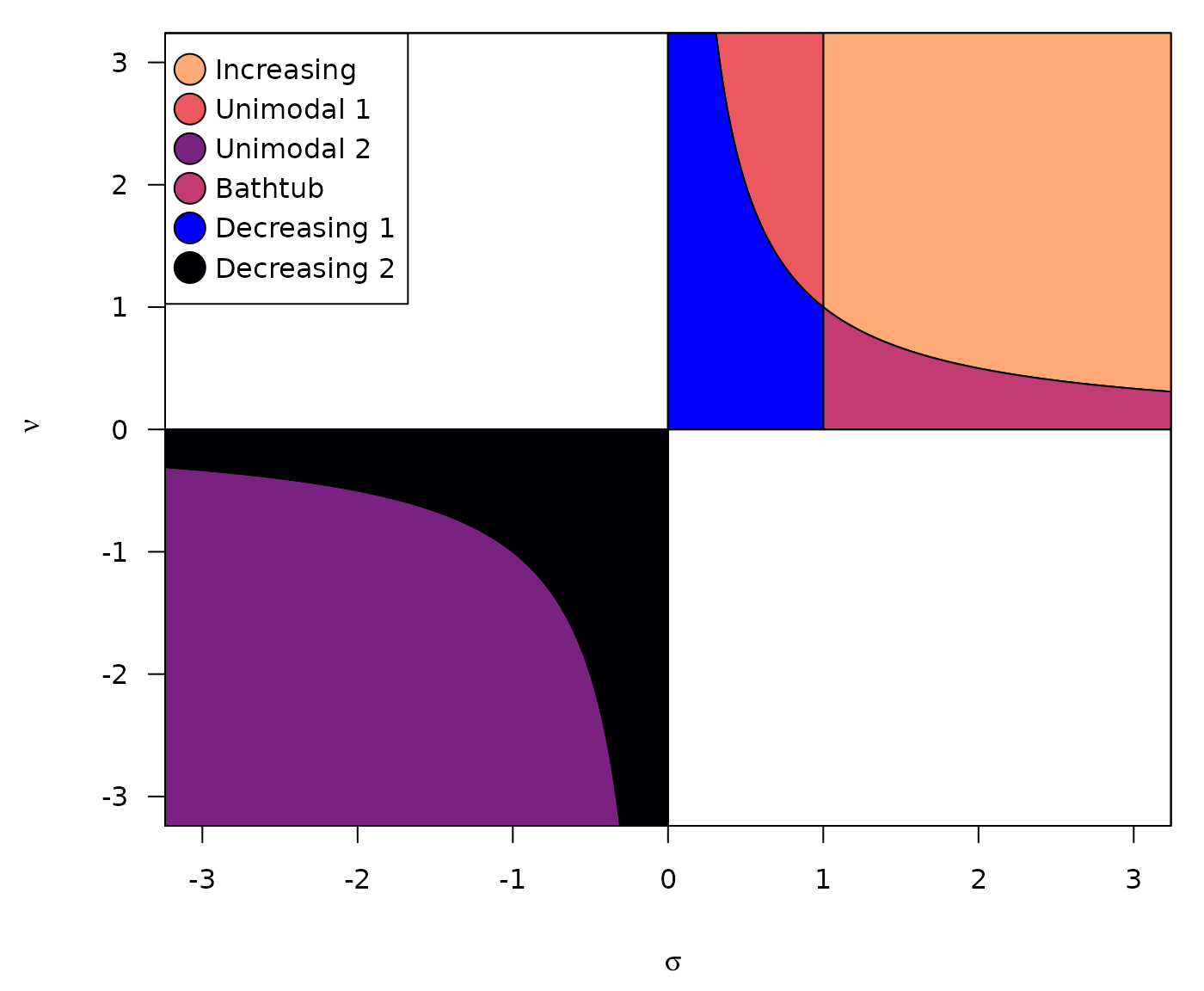
Application examples

Time to failure on electronic equipment

Cooray (2015) used the following data provided by Wang (2000) in order to fit an OW distribution through maximum likelihood estimation (MLE):

5, 11, 21, 31, 46, 75, 98, 122, 145, 165, 195, 224, 245, 293, 321, 330, 350, 420.

The data above is the time to failure of an electronic device in hours. As an alternative to classical MLE, We used the function to fit an only-intercept model in order to estimate parameters of OW distribution without covariates. Using our initValuesOW(), we can obtain an initial guess and the valid region.

data("equipment")
my_initial_guess <- initValuesOW(formula = equipment ~ 1)

summary(my_initial_guess)
#> --------------------------------------------------------------------
#> Initial Values
#> sigma = 5
#> nu = 0.1
#> --------------------------------------------------------------------
#> Search Regions
#> For sigma: all(sigma > 1)
#> For nu: all(nu < 1/sigma)
#> --------------------------------------------------------------------
#> Hazard shape: Bathtub

initValuesOW() function detected the Bathtub hazard shape, which corresponds to a convex-then-concave shape of total time on test (TTT) plot

old_par <- par(mfrow = c(1, 1)) # save previous graphical parameters

par(mar = c(3.7, 3.7, 1, 10), mgp = c(2.5, 1, 0))
plot(my_initial_guess, las = 1)
legend.HazardShape(x = 1.07, y = 1.04, xpd = TRUE)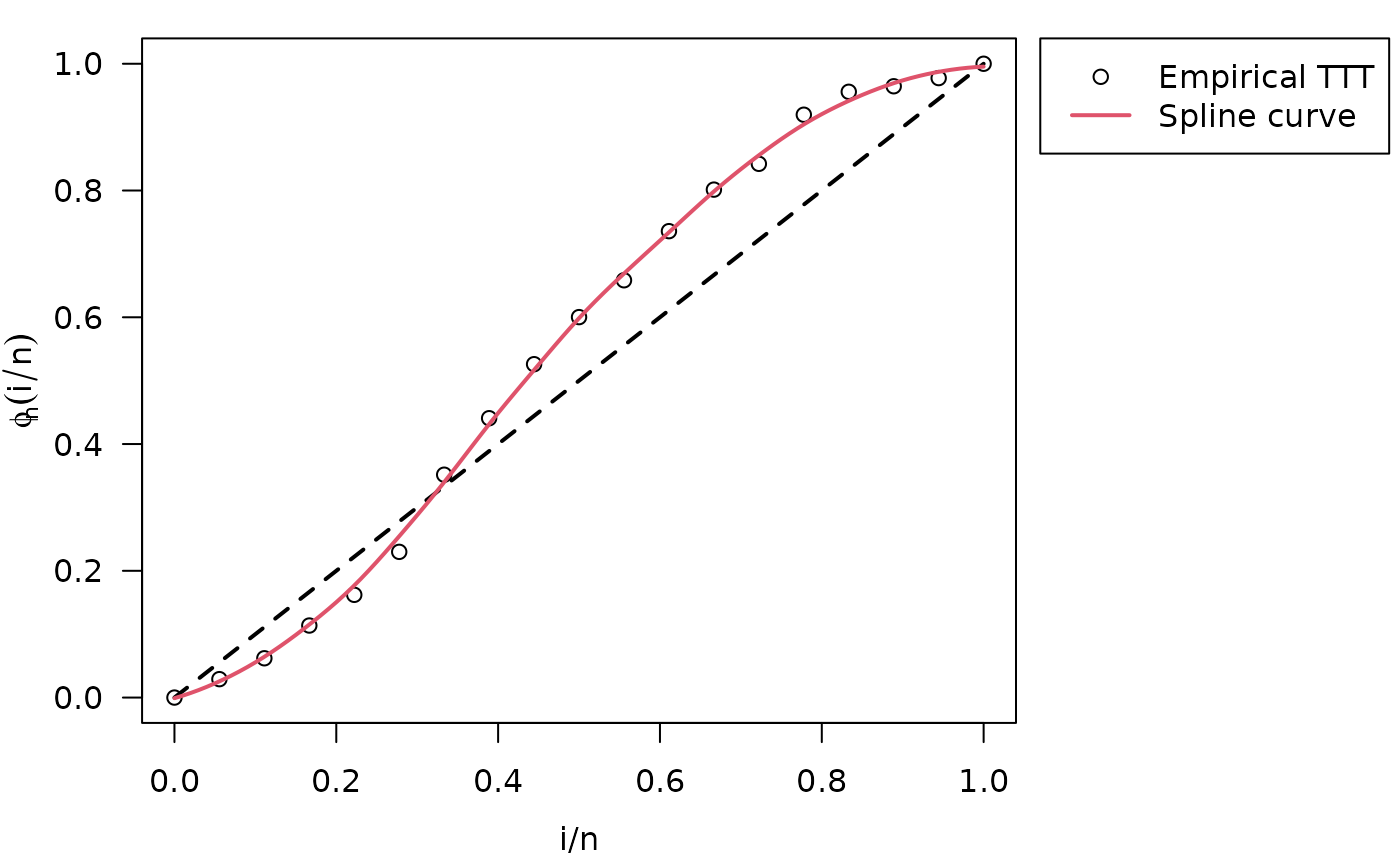


par(old_par) # restore previous graphical parameters

Therefore, we define the search region according to initValuesOW() outputs

# Custom search region
myvalues <- list(sigma = "all(sigma > 1)",
                 nu = "all(nu < 1/sigma)")

and we perform the fit using gamlss()

# gamlss set up
con.out <-gamlss.control(n.cyc = 300, trace=TRUE)
myOW <- myOW_region(family = OW(sigma.link='identity'),
                    valid.values = myvalues, initVal = my_initial_guess)

param_ee <- gamlss(equipment ~ 1, sigma.fo = ~ 1, nu.fo = ~ 1, 
                   sigma.start = 5, nu.start = 0.1,
                   control = con.out, family = myOW)
#> GAMLSS-RS iteration 1: Global Deviance = 220.3699 
#> GAMLSS-RS iteration 2: Global Deviance = 218.2162 
#> GAMLSS-RS iteration 3: Global Deviance = 217.5282 
#> GAMLSS-RS iteration 4: Global Deviance = 217.3291 
#> GAMLSS-RS iteration 5: Global Deviance = 217.2142 
#> GAMLSS-RS iteration 6: Global Deviance = 217.1047 
#> GAMLSS-RS iteration 7: Global Deviance = 216.9932 
#> GAMLSS-RS iteration 8: Global Deviance = 216.8872 
#> GAMLSS-RS iteration 9: Global Deviance = 216.7914 
#> GAMLSS-RS iteration 10: Global Deviance = 216.707 
#> GAMLSS-RS iteration 11: Global Deviance = 216.6337 
#> GAMLSS-RS iteration 12: Global Deviance = 216.5706 
#> GAMLSS-RS iteration 13: Global Deviance = 216.5168 
#> GAMLSS-RS iteration 14: Global Deviance = 216.471 
#> GAMLSS-RS iteration 15: Global Deviance = 216.4324 
#> GAMLSS-RS iteration 16: Global Deviance = 216.3997 
#> GAMLSS-RS iteration 17: Global Deviance = 216.3723 
#> GAMLSS-RS iteration 18: Global Deviance = 216.3492 
#> GAMLSS-RS iteration 19: Global Deviance = 216.3299 
#> GAMLSS-RS iteration 20: Global Deviance = 216.3136 
#> GAMLSS-RS iteration 21: Global Deviance = 216.3 
#> GAMLSS-RS iteration 22: Global Deviance = 216.2885 
#> GAMLSS-RS iteration 23: Global Deviance = 216.2789 
#> GAMLSS-RS iteration 24: Global Deviance = 216.2708 
#> GAMLSS-RS iteration 25: Global Deviance = 216.264 
#> GAMLSS-RS iteration 26: Global Deviance = 216.2583 
#> GAMLSS-RS iteration 27: Global Deviance = 216.2533 
#> GAMLSS-RS iteration 28: Global Deviance = 216.2488 
#> GAMLSS-RS iteration 29: Global Deviance = 216.245 
#> GAMLSS-RS iteration 30: Global Deviance = 216.2418 
#> GAMLSS-RS iteration 31: Global Deviance = 216.2391 
#> GAMLSS-RS iteration 32: Global Deviance = 216.2369 
#> GAMLSS-RS iteration 33: Global Deviance = 216.2351 
#> GAMLSS-RS iteration 34: Global Deviance = 216.2336 
#> GAMLSS-RS iteration 35: Global Deviance = 216.232 
#> GAMLSS-RS iteration 36: Global Deviance = 216.2306 
#> GAMLSS-RS iteration 37: Global Deviance = 216.2294 
#> GAMLSS-RS iteration 38: Global Deviance = 216.2284
summary(param_ee)
#> ******************************************************************
#> Family:  c("OW", "Odd Weibull") 
#> 
#> Call:  gamlss(formula = equipment ~ 1, sigma.formula = ~1,  
#>     nu.formula = ~1, family = myOW, sigma.start = 5,  
#>     nu.start = 0.1, control = con.out) 
#> 
#> Fitting method: RS() 
#> 
#> ------------------------------------------------------------------
#> Mu link function:  log
#> Mu Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   -5.240      0.205  -25.56 8.79e-14 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> Sigma link function:  identity
#> Sigma Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)  
#> (Intercept)    3.283      1.423   2.307   0.0357 *
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> Nu link function:  log 
#> Nu Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)  
#> (Intercept)  -1.2715     0.5019  -2.534   0.0229 *
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> No. of observations in the fit:  18 
#> Degrees of Freedom for the fit:  3
#>       Residual Deg. of Freedom:  15 
#>                       at cycle:  38 
#>  
#> Global Deviance:     216.2284 
#>             AIC:     222.2284 
#>             SBC:     224.8996 
#> ******************************************************************

In the following table we summarize the results and compare them with those gotten by Cooray (2015)

Parameter	MLE (Cooray 2015)	GAMLSS
$\mu$	5.35e-03	5.30e-03
$\sigma$	3.22388	3.2828
$\nu$	0.28424	0.2804

Mortality in mice exposed to radiation

Cooray (2006) used a dataset with 208 data points provided by Kimball (1960) with the ages at death in weeks for male mice exposed to 240r of gamma radiation. Again, we implement a workflow for parameter estimation with myOW_region and gamlss functions.

# Do not forget to load 'RelDists' package
data("mice")
init_vals <- initValuesOW(formula = mice ~ 1)

summary(init_vals)
#> --------------------------------------------------------------------
#> Initial Values
#> sigma = 2
#> nu = 6
#> --------------------------------------------------------------------
#> Search Regions
#> For sigma: all(sigma > 1)
#> For nu: all(nu > 1/sigma)
#> --------------------------------------------------------------------
#> Hazard shape: Increasing

With initValuesOW() function we identified an increasing hazard shape, as well as was stated by Cooray (2006), because TTT plot is concave.

old_par <- par(mfrow = c(1, 1)) # save previous graphical parameters

par(mar = c(3.7, 3.7, 1, 10), mgp = c(2.5, 1, 0))
plot(init_vals, las = 1)
legend.HazardShape(x = 1.07, y = 1.04, xpd = TRUE)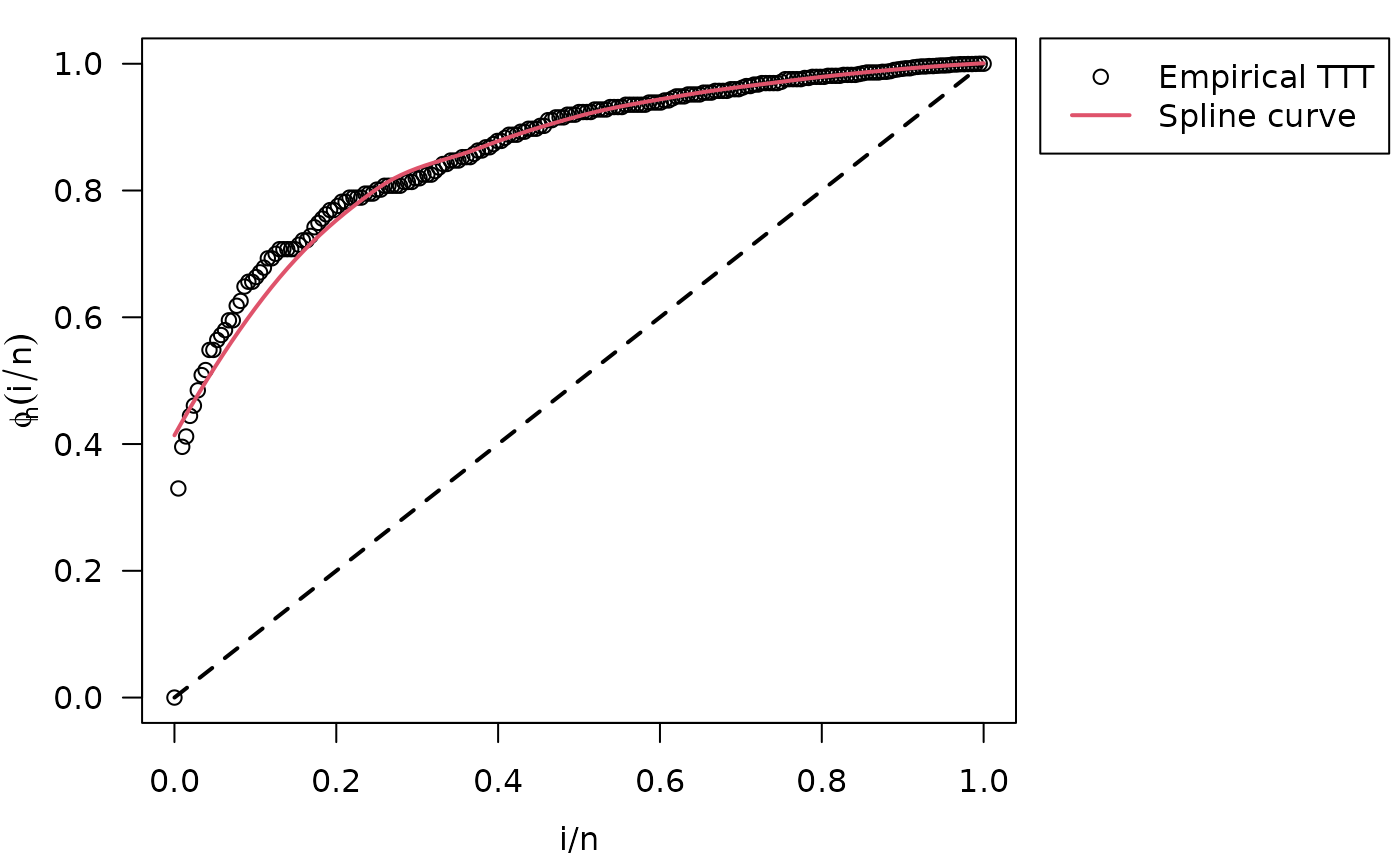


par(old_par) # restore previous graphical parameters

Hence, we implement the estimation procedure

# gamlss set up
myOW <- myOW_region(initVal = init_vals)

# Custom search region
# Do not forget to load 'gamlss' library
param_mm <- gamlss(mice ~ 1, sigma.fo = ~ 1, nu.fo = ~ 1,
                   sigma.start = 2, nu.start = 6,
                   control = con.out,
                   family = myOW)
#> GAMLSS-RS iteration 1: Global Deviance = 2031.511 
#> GAMLSS-RS iteration 2: Global Deviance = 2006.257 
#> GAMLSS-RS iteration 3: Global Deviance = 2005.168 
#> GAMLSS-RS iteration 4: Global Deviance = 2005.063 
#> GAMLSS-RS iteration 5: Global Deviance = 2004.941 
#> GAMLSS-RS iteration 6: Global Deviance = 2004.817 
#> GAMLSS-RS iteration 7: Global Deviance = 2004.69 
#> GAMLSS-RS iteration 8: Global Deviance = 2004.558 
#> GAMLSS-RS iteration 9: Global Deviance = 2004.423 
#> GAMLSS-RS iteration 10: Global Deviance = 2004.283 
#> GAMLSS-RS iteration 11: Global Deviance = 2004.139 
#> GAMLSS-RS iteration 12: Global Deviance = 2003.991 
#> GAMLSS-RS iteration 13: Global Deviance = 2003.838 
#> GAMLSS-RS iteration 14: Global Deviance = 2003.68 
#> GAMLSS-RS iteration 15: Global Deviance = 2003.517 
#> GAMLSS-RS iteration 16: Global Deviance = 2003.348 
#> GAMLSS-RS iteration 17: Global Deviance = 2003.174 
#> GAMLSS-RS iteration 18: Global Deviance = 2002.993 
#> GAMLSS-RS iteration 19: Global Deviance = 2002.807 
#> GAMLSS-RS iteration 20: Global Deviance = 2002.613 
#> GAMLSS-RS iteration 21: Global Deviance = 2002.413 
#> GAMLSS-RS iteration 22: Global Deviance = 2002.205 
#> GAMLSS-RS iteration 23: Global Deviance = 2001.989 
#> GAMLSS-RS iteration 24: Global Deviance = 2001.766 
#> GAMLSS-RS iteration 25: Global Deviance = 2001.533 
#> GAMLSS-RS iteration 26: Global Deviance = 2001.292 
#> GAMLSS-RS iteration 27: Global Deviance = 2001.041 
#> GAMLSS-RS iteration 28: Global Deviance = 2000.78 
#> GAMLSS-RS iteration 29: Global Deviance = 2000.507 
#> GAMLSS-RS iteration 30: Global Deviance = 2000.224 
#> GAMLSS-RS iteration 31: Global Deviance = 1999.929 
#> GAMLSS-RS iteration 32: Global Deviance = 1999.621 
#> GAMLSS-RS iteration 33: Global Deviance = 1999.299 
#> GAMLSS-RS iteration 34: Global Deviance = 1998.964 
#> GAMLSS-RS iteration 35: Global Deviance = 1998.613 
#> GAMLSS-RS iteration 36: Global Deviance = 1998.247 
#> GAMLSS-RS iteration 37: Global Deviance = 1997.864 
#> GAMLSS-RS iteration 38: Global Deviance = 1997.463 
#> GAMLSS-RS iteration 39: Global Deviance = 1997.037 
#> GAMLSS-RS iteration 40: Global Deviance = 1996.591 
#> GAMLSS-RS iteration 41: Global Deviance = 1996.124 
#> GAMLSS-RS iteration 42: Global Deviance = 1995.634 
#> GAMLSS-RS iteration 43: Global Deviance = 1995.121 
#> GAMLSS-RS iteration 44: Global Deviance = 1994.584 
#> GAMLSS-RS iteration 45: Global Deviance = 1994.022 
#> GAMLSS-RS iteration 46: Global Deviance = 1993.434 
#> GAMLSS-RS iteration 47: Global Deviance = 1992.822 
#> GAMLSS-RS iteration 48: Global Deviance = 1992.183 
#> GAMLSS-RS iteration 49: Global Deviance = 1991.518 
#> GAMLSS-RS iteration 50: Global Deviance = 1990.826 
#> GAMLSS-RS iteration 51: Global Deviance = 1990.111 
#> GAMLSS-RS iteration 52: Global Deviance = 1989.373 
#> GAMLSS-RS iteration 53: Global Deviance = 1988.617 
#> GAMLSS-RS iteration 54: Global Deviance = 1987.847 
#> GAMLSS-RS iteration 55: Global Deviance = 1987.068 
#> GAMLSS-RS iteration 56: Global Deviance = 1986.285 
#> GAMLSS-RS iteration 57: Global Deviance = 1985.506 
#> GAMLSS-RS iteration 58: Global Deviance = 1984.74 
#> GAMLSS-RS iteration 59: Global Deviance = 1983.994 
#> GAMLSS-RS iteration 60: Global Deviance = 1983.277 
#> GAMLSS-RS iteration 61: Global Deviance = 1982.597 
#> GAMLSS-RS iteration 62: Global Deviance = 1981.963 
#> GAMLSS-RS iteration 63: Global Deviance = 1981.381 
#> GAMLSS-RS iteration 64: Global Deviance = 1980.854 
#> GAMLSS-RS iteration 65: Global Deviance = 1980.384 
#> GAMLSS-RS iteration 66: Global Deviance = 1979.972 
#> GAMLSS-RS iteration 67: Global Deviance = 1979.619 
#> GAMLSS-RS iteration 68: Global Deviance = 1979.317 
#> GAMLSS-RS iteration 69: Global Deviance = 1979.062 
#> GAMLSS-RS iteration 70: Global Deviance = 1978.85 
#> GAMLSS-RS iteration 71: Global Deviance = 1978.676 
#> GAMLSS-RS iteration 72: Global Deviance = 1978.533 
#> GAMLSS-RS iteration 73: Global Deviance = 1978.417 
#> GAMLSS-RS iteration 74: Global Deviance = 1978.324 
#> GAMLSS-RS iteration 75: Global Deviance = 1978.25 
#> GAMLSS-RS iteration 76: Global Deviance = 1978.192 
#> GAMLSS-RS iteration 77: Global Deviance = 1978.146 
#> GAMLSS-RS iteration 78: Global Deviance = 1978.112 
#> GAMLSS-RS iteration 79: Global Deviance = 1978.085 
#> GAMLSS-RS iteration 80: Global Deviance = 1978.064 
#> GAMLSS-RS iteration 81: Global Deviance = 1978.047 
#> GAMLSS-RS iteration 82: Global Deviance = 1978.034 
#> GAMLSS-RS iteration 83: Global Deviance = 1978.024 
#> GAMLSS-RS iteration 84: Global Deviance = 1978.016 
#> GAMLSS-RS iteration 85: Global Deviance = 1978.01 
#> GAMLSS-RS iteration 86: Global Deviance = 1978.005 
#> GAMLSS-RS iteration 87: Global Deviance = 1978.001 
#> GAMLSS-RS iteration 88: Global Deviance = 1977.998 
#> GAMLSS-RS iteration 89: Global Deviance = 1977.996 
#> GAMLSS-RS iteration 90: Global Deviance = 1977.994 
#> GAMLSS-RS iteration 91: Global Deviance = 1977.992 
#> GAMLSS-RS iteration 92: Global Deviance = 1977.991 
#> GAMLSS-RS iteration 93: Global Deviance = 1977.99
summary(param_mm)
#> ******************************************************************
#> Family:  c("OW", "Odd Weibull") 
#> 
#> Call:  gamlss(formula = mice ~ 1, sigma.formula = ~1, nu.formula = ~1,  
#>     family = myOW, sigma.start = 2, nu.start = 6, control = con.out) 
#> 
#> Fitting method: RS() 
#> 
#> ------------------------------------------------------------------
#> Mu link function:  log
#> Mu Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -4.87857    0.01489  -327.6   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> Sigma link function:  log
#> Sigma Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)   1.8206     0.1349    13.5   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> Nu link function:  log 
#> Nu Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)  
#> (Intercept)  -0.2794     0.1640  -1.704     0.09 .
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> ------------------------------------------------------------------
#> No. of observations in the fit:  208 
#> Degrees of Freedom for the fit:  3
#>       Residual Deg. of Freedom:  205 
#>                       at cycle:  93 
#>  
#> Global Deviance:     1977.99 
#>             AIC:     1983.99 
#>             SBC:     1994.003 
#> ******************************************************************

Then, we report the results and compare them with those in Cooray (2006)

Parameter	MLE (Cooray 2006)	GAMLSS
$\mu$	7.61e-03	7.61e-03
$\sigma$	6.2278	6.1754
$\nu$	0.7495	0.7563

References

Cooray, Kahadawala. 2006. “Generalization of the Weibull distribution: The odd Weibull family.” Statistical Modelling 6 (3): 265–77. https://doi.org/10.1191/1471082X06st116oa.

———. 2015. “A study of moments and likelihood estimators of the odd Weibull distribution.” Statistical Methodology 26 (September): 72–83. https://doi.org/10.1016/j.stamet.2015.03.003.

Kimball, A. W. 1960. “Estimation of Mortality Intensities in Animal Experiments.” Biometrics 16 (4): 505. https://doi.org/10.2307/2527758.

Wang, F. K. 2000. “A new model with bath tub-shaped failure rate using an additive Burr XII distribution.” Reliability Engineering and System Safety 70 (3): 305–12. https://doi.org/10.1016/S0951-8320(00)00066-1.

Jaime Mosquera

2024-07-09

Odd Weibull distribution

Application examples

Time to failure on electronic equipment

Mortality in mice exposed to radiation

References