FWE distribution

Freddy Hernandez

2024-07-09

library(RelDists)
#> Loading required package: survival
#> Loading required package: EstimationTools
#> Loading required package: DEoptim
#> Loading required package: parallel
#> 
#> DEoptim package
#> Differential Evolution algorithm in R
#> Authors: D. Ardia, K. Mullen, B. Peterson and J. Ulrich
#> Loading required package: BBmisc
#> 
#> Attaching package: 'BBmisc'
#> The following object is masked from 'package:base':
#> 
#>     isFALSE
#> Loading required package: GA
#> Loading required package: foreach
#> Loading required package: iterators
#> Package 'GA' version 3.2.4
#> Type 'citation("GA")' for citing this R package in publications.
#> 
#> Attaching package: 'GA'
#> The following object is masked from 'package:utils':
#> 
#>     de
#> Loading required package: gaussquad
#> Loading required package: orthopolynom
#> 
#> 
#> ><<<<<<<<<<<<<<<<<<<<<<<<   EstimationTools Version 4.0.0   >>>>>>>>>>>>>>>>>>>>>>>><
#>   Feel free to report bugs in https://github.com/Jaimemosg/EstimationTools/issues

Flexible Weibull extension distribution

This distribution was proposed by Bebbington (2007). The probability density function $f(x)$ and cumulative density function $F(x)$ are given by:

$$f(x) = \left( \mu+ \frac{\sigma}{x^2} \right) e^{\mu x - \sigma / x} \exp \left( -e^{\mu x - \sigma / x} \right),$$

and

$$F(x) = 1 - \exp[-e^{\mu x - \sigma / x}], \quad x > 0.$$

respectively, where $\mu > 0$, $\sigma > 0$ and $x > 0$.

Next figure shows possible shapes of the $f(x)$ and $F(x)$ for several values of the parameters.

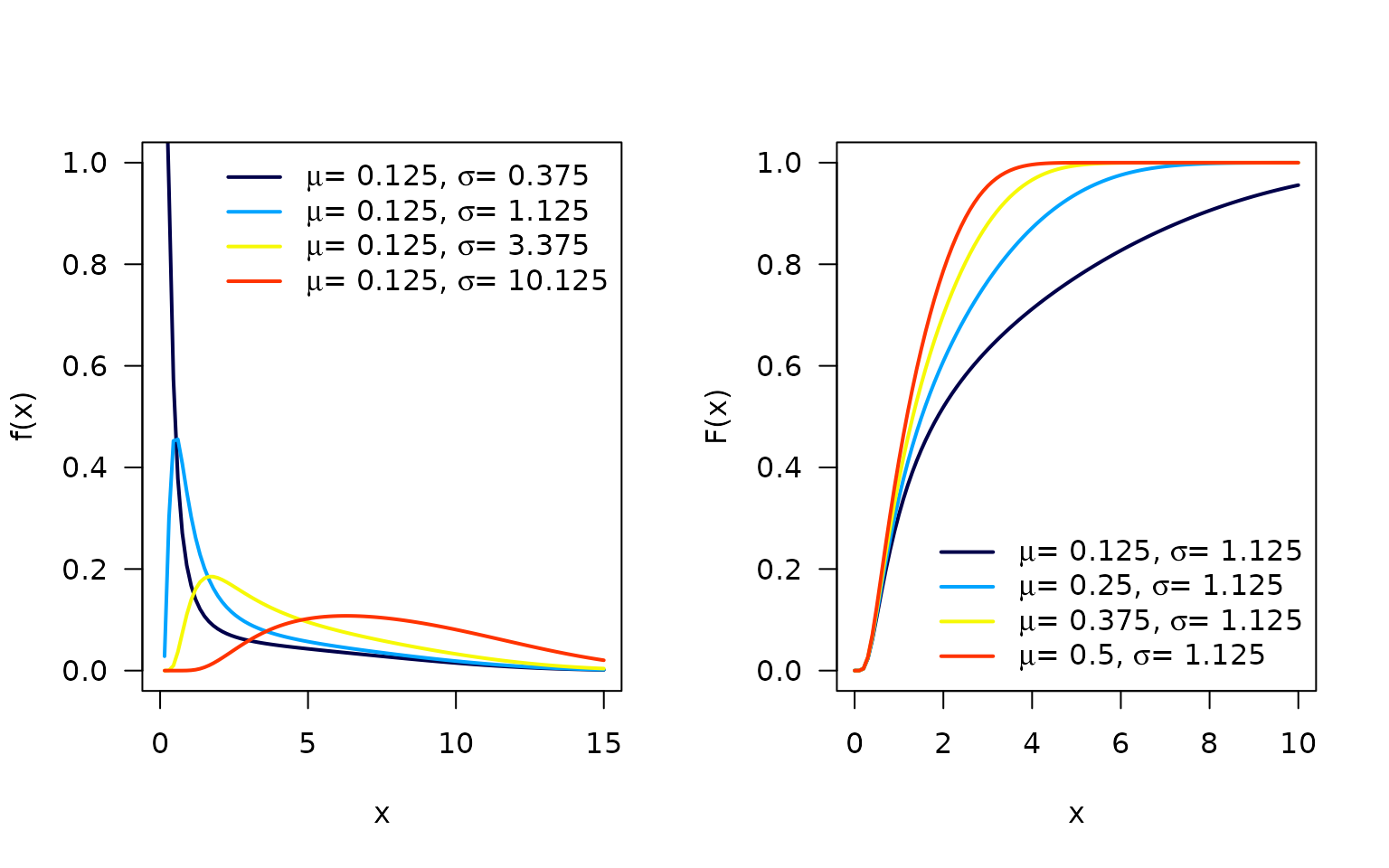
Bebbington, M., C. D. Lai, and R. Zitikis. 2007. “A Flexible Weibull Extension.” Reliability Engineering & System Safety 92 (6): 719–26.