Density, distribution function, quantile function,
random generation and hazard function for the Extended Odd Fr?chet-Nadarajah-Haghighi distribution
with parameters mu, sigma, nu and tau.
Usage
dEOFNH(x, mu, sigma, nu, tau, log = FALSE)
pEOFNH(q, mu, sigma, nu, tau, lower.tail = TRUE, log.p = FALSE)
qEOFNH(p, mu, sigma, nu, tau, lower.tail = TRUE, log.p = FALSE)
rEOFNH(n, mu, sigma, nu, tau)
hEOFNH(x, mu, sigma, nu, tau)Arguments
- x, q
vector of quantiles.
- mu
parameter.
- sigma
parameter.
- nu
parameter.
- tau
parameter.
- log, log.p
logical; if TRUE, probabilities p are given as log(p).
- lower.tail
logical; if TRUE (default), probabilities are P[X <= x], otherwise, P[X > x].
- p
vector of probabilities.
- n
number of observations.
Value
dEOFNH gives the density, pEOFNH gives the distribution
function, qEOFNH gives the quantile function, rEOFNH
generates random numbers and hEOFNH gives the hazard function.
Details
Tthe Extended Odd Frechet-Nadarajah-Haghighi mu,
sigma, nu and tau has density given by
\(f(x)= \frac{\mu\sigma\nu\tau(1+\nu x)^{\sigma-1}e^{(1-(1+\nu x)^\sigma)}[1-(1-e^{(1-(1+\nu x)^\sigma)})^{\mu}]^{\tau-1}}{(1-e^{(1-(1+\nu x)^{\sigma})})^{\mu\tau+1}} e^{-[(1-e^{(1-(1+\nu x)^\sigma)})^{-\mu}-1]^{\tau}},\)
for \(x > 0\), \(\mu > 0\), \(\sigma > 0\), \(\nu > 0\) and \(\tau > 0\).
References
Nasiru S (2018). “Extended Odd Fréchet-G Family of Distributions.” Journal of Probability and Statistics, 2018.
Examples
old_par <- par(mfrow = c(1, 1)) # save previous graphical parameters
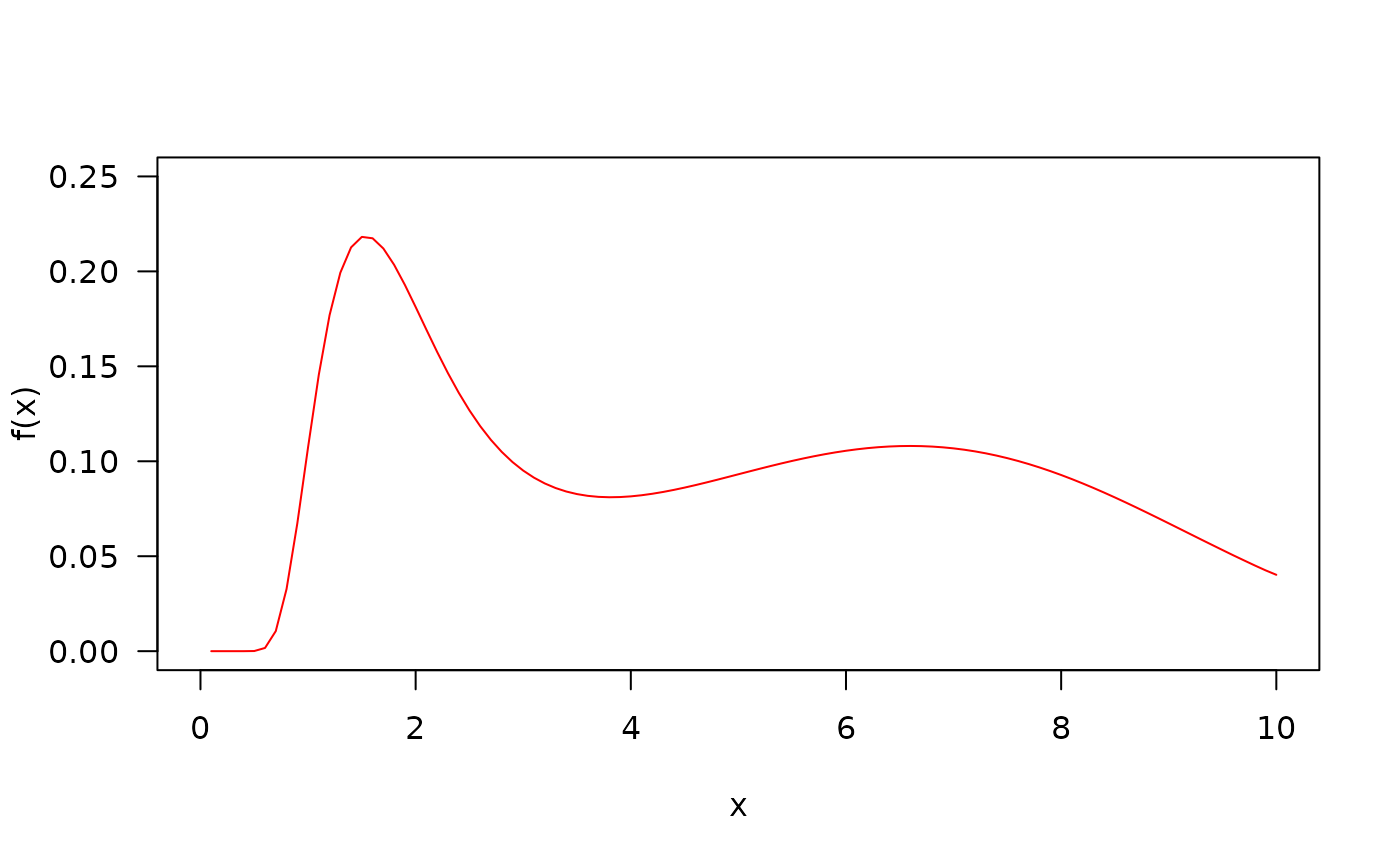
##The probability density function
par(mfrow=c(1,1))
curve(dEOFNH(x, mu=18.5, sigma=5.1, nu=0.1, tau=0.1), from=0, to=10,
ylim=c(0, 0.25), col="red", las=1, ylab="f(x)")
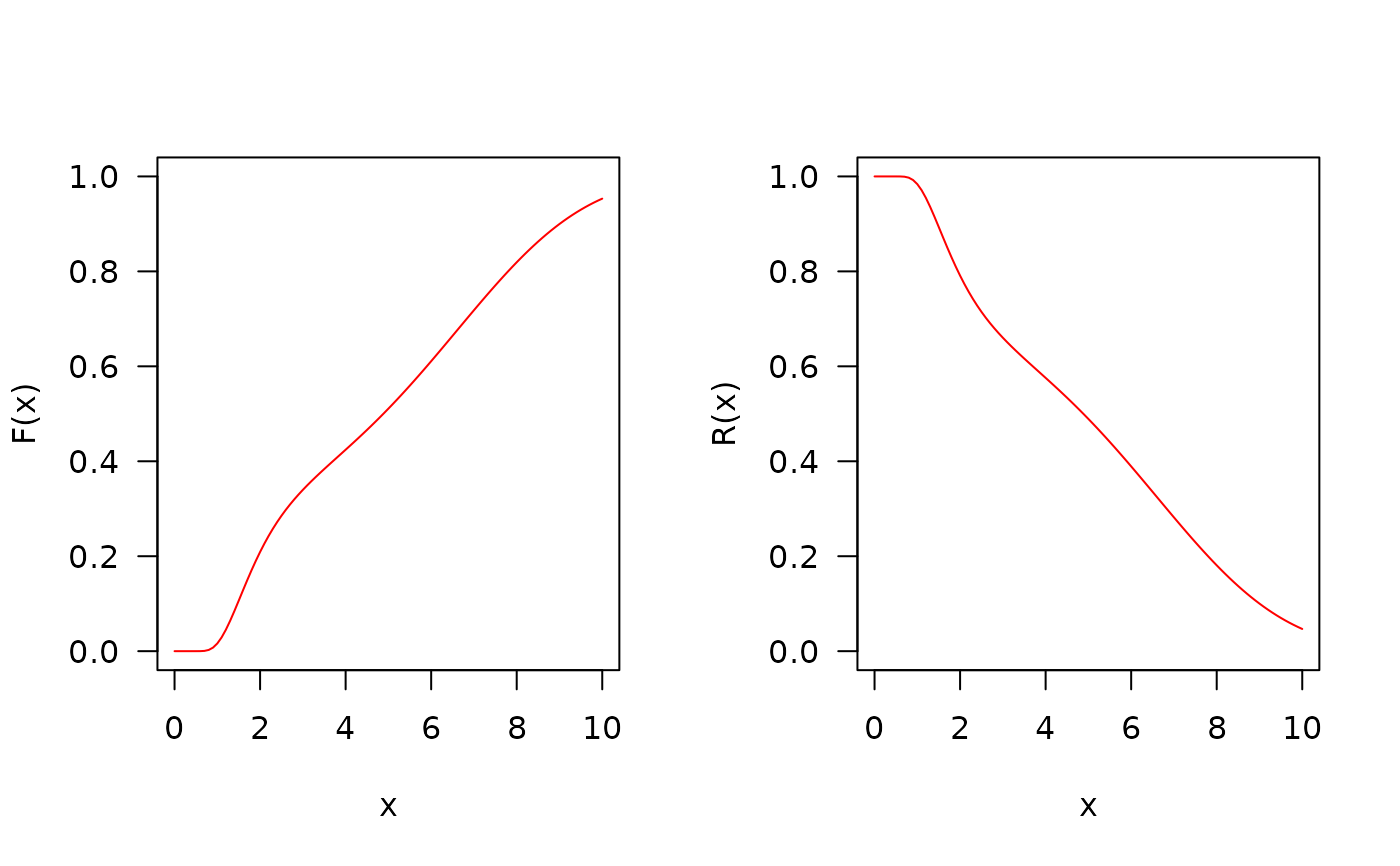
## The cumulative distribution and the Reliability function
par(mfrow = c(1, 2))
curve(pEOFNH(x,mu=18.5, sigma=5.1, nu=0.1, tau=0.1), from = 0, to = 10,
ylim = c(0, 1), col = "red", las = 1, ylab = "F(x)")
curve(pEOFNH(x, mu=18.5, sigma=5.1, nu=0.1, tau=0.1, lower.tail = FALSE),
from = 0, to = 10, ylim = c(0, 1), col = "red", las = 1, ylab = "R(x)")
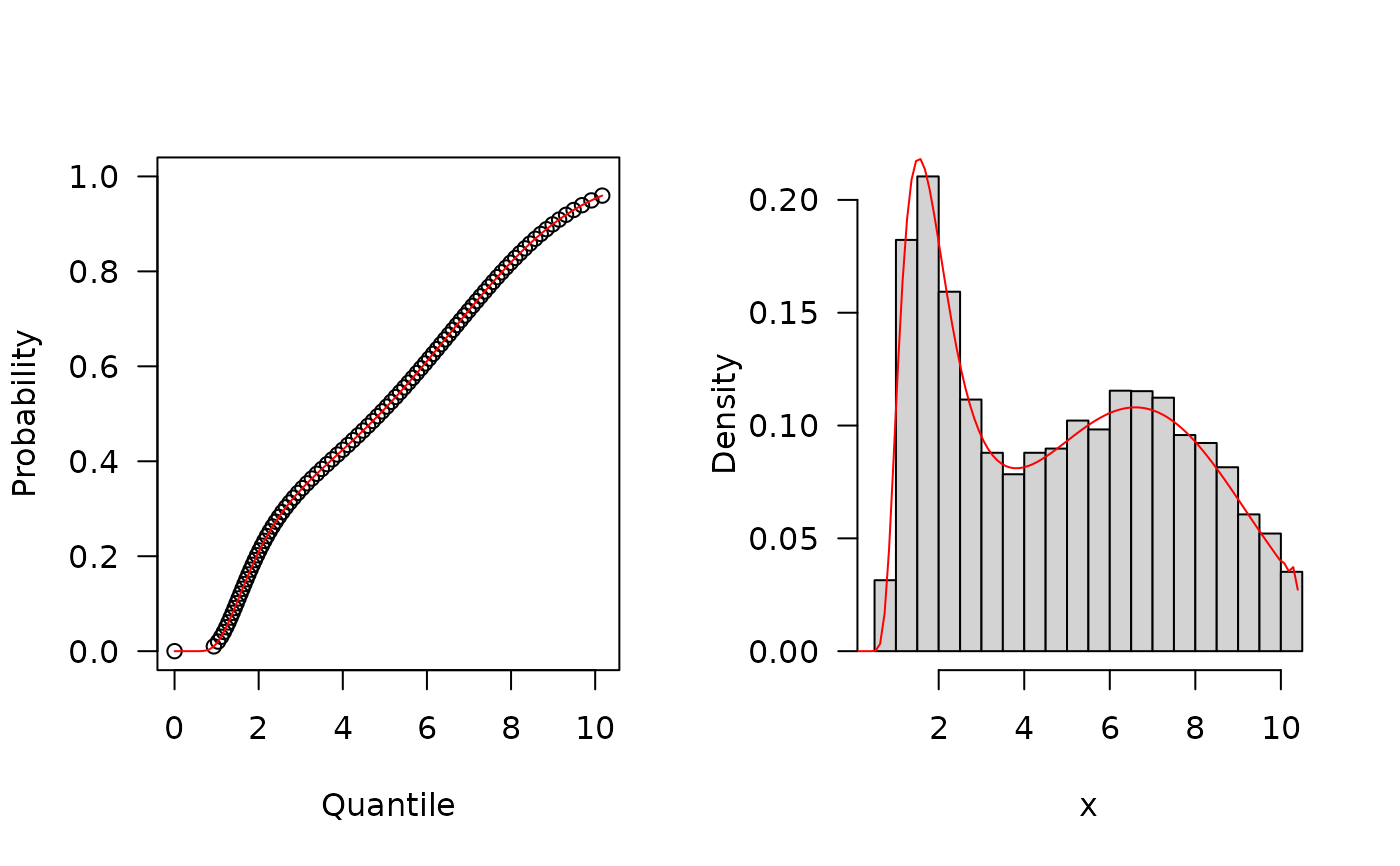
##The quantile function
p <- seq(from=0, to=0.99999, length.out=100)
plot(x=qEOFNH(p, mu=18.5, sigma=5.1, nu=0.1, tau=0.1), y=p, xlab="Quantile",
las=1, ylab="Probability")
curve(pEOFNH(x, mu=18.5, sigma=5.1, nu=0.1, tau=0.1), from=0, add=TRUE, col="red")
##The random function
hist(rEOFNH(n=10000, mu=18.5, sigma=5.1, nu=0.1, tau=0.1), freq=FALSE,
xlab="x", las=1, main="")
curve(dEOFNH(x, mu=18.5, sigma=5.1, nu=0.1, tau=0.1), from=0, add=TRUE, col="red", ylim=c(0,1.25))
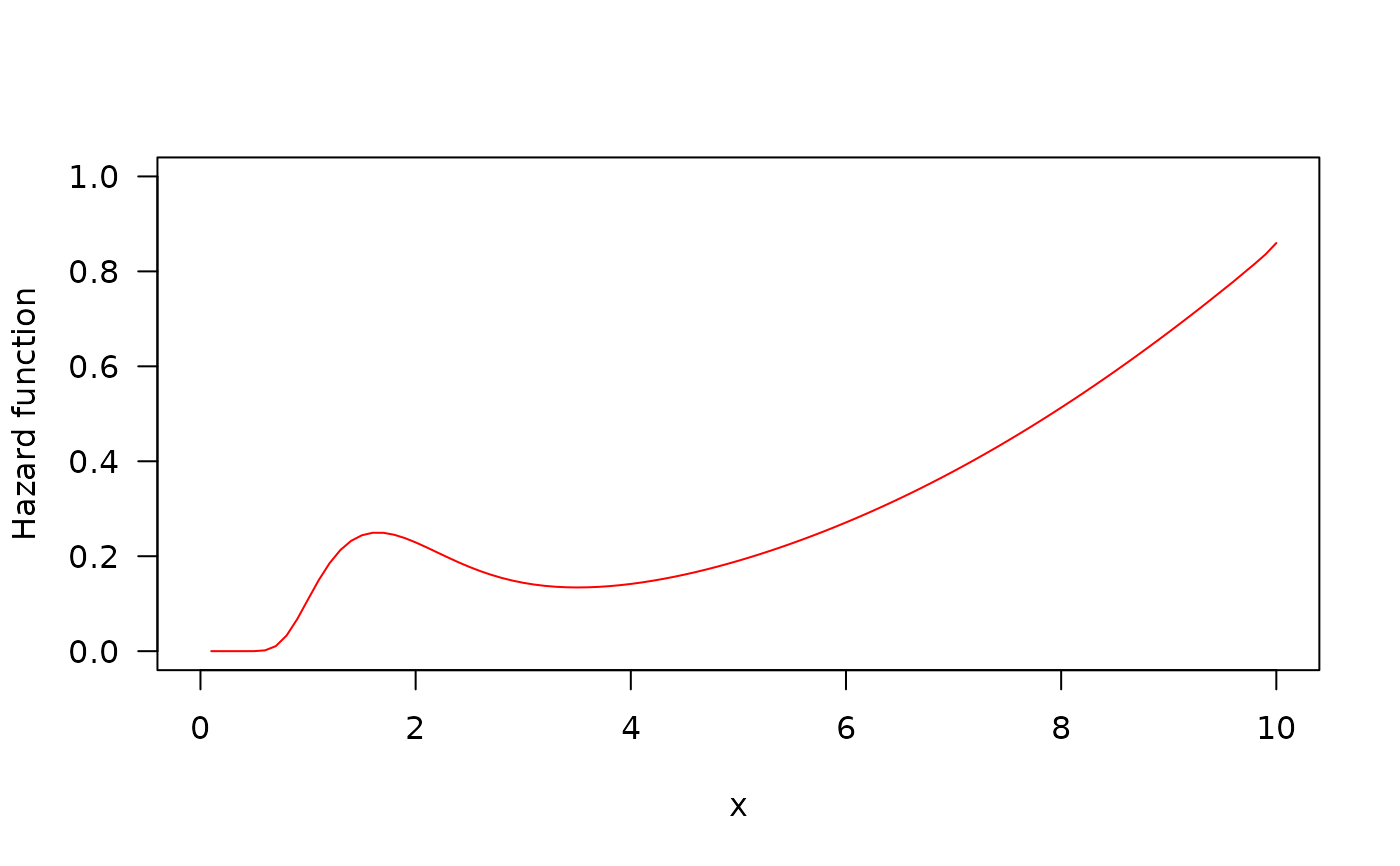
##The Hazard function
par(mfrow=c(1,1))
curve(hEOFNH(x, mu=18.5, sigma=5.1, nu=0.1, tau=0.1), from=0, to=10, ylim=c(0, 1),
col="red", ylab="Hazard function", las=1)
par(old_par) # restore previous graphical parameters